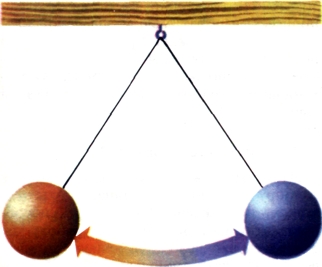
После одного колебания восстанавливается исходное состояние.
Г. Линднер КАРТИНЫ СОВРЕМЕННОЙ ФИЗИКИ (с большими сокращениями) МОСКВА "МИР" 1977 |
Мы познакомились с законом сохранения энергии, одним из наиболее всеобъемлющих физических принципов, мы видели также, что он гармонично сочетается с законом сохранения массы. Однако достаточен ли этот закон для того, чтобы полностью объяснить ход процессов в природе? Два элементарных примера покажут нам, что он нуждается в важном дополнении.
 |
|
Рис. 65. Обратимый процесс. После одного колебания восстанавливается исходное состояние. |
Рассмотрим простой математический маятник (рис. 65). В высшей точке своей траектории он обладает потенциальной энергией. Когда маятник проскакивает через низшую точку, потенциальная энергия переходит в кинетическую. Затем маятник вновь попадает в высшую точку (но уже с другой стороны от положения равновесия), где он опять имеет лишь потенциальную энергию. Таким образом, здесь мы сталкиваемся с обратимым процессом. После продолжающегося некоторое время взаимопревращения энергии вновь полностью восстанавливается начальное состояние.
Совершенно иначе обстоит дело, например, с печью. Каждая калория, отданная ее горячей поверхностью, обнаруживается в нагретом воздухе комнаты. С точки зрения закона сохранения энергии здесь все в полном порядке. Но этот закон не нарушился бы ни на йоту, если бы теплота, содержащаяся в воздухе, снова «перекочевала» к печи и ее остывшие стенки вновь нагрелись. Однако против этого восстает весь накопленный с незапамятных времен человеческий опыт: тепловая энергия самопроизвольно переходит всегда лишь от более горячих тел к более холодным, и никогда — в обратном направлении. Без сомнения, здесь мы имеем дело с необратимым процессом (рис. 66).
 |
|
Рис. 66. Небратимый процесс.
|
Совершенно аналогичные рассуждения справедливы и применительно к экспериментам с газами. Если мы, например, адиабатически сожмем находящийся в цилиндре газ, а затем внезапно отпустим поршень, он устремится вверх, как будто его тянет какая-то невидимая пружина. Объем, давление и температура газа вновь принимают первоначальные значения. Содержащаяся в объеме газа тепловая энергия снова превращается в механическую работу. Таким образом, адиабатический процесс оказывается вполне обратимым.
Напротив, изотермическое сжатие, несомненно, представляет собой необратимый процесс. Образующееся при сжатии тепло безвозвратно «утекает» сквозь стенки цилиндра. Оно уже никогда самопроизвольно не вернется в цилиндр и не превратится в механическую работу. Это объясняется тем, что для «вытекания» тепла из цилиндра достаточно, чтобы температура в окружающем пространстве была ниже, чем внутри цилиндра. И, как мы уже видели в примере с печью, тепло никогда не передается в противоположном направлении.
Теперь представим, что перепад температур бесконечно мал, а внешний термостат, окружающий цилиндр, бесконечно велик. В этой, весьма искусственной, ситуации поток тепла может беспрепятственно перетекать в обоих направлениях, и температура при этом не изменяется. Такой процесс фактически является обратимым. Разумеется, в действительности подобный процесс неосуществим; однако в теоретических рассмотрениях он играет важную роль.
Итак, в природе существуют два вида процессов, которые различаются принципиально. Макс Планк сказал однажды, что «различие между обратимыми и необратимыми процессами лежит гораздо глубже, чем, например, между процессами механическими и электрическими; поэтому именно его с большим основанием, чем любой другой признак, следовало бы выбрать в качестве первейшего принципа при классификации физических явлений».
Теплота передается лишь от печки в комнату, но никогда в обратном направлении.
То, что в действительности не существует в строгом смысле слова обратимых процессов, не должно нас смущать. Во всех механических процессах, в том числе в приведенных нами примерах, невозможно избежать трения или передачи тепла. Лишь в мысленном эксперименте можно построить полностью обратимые процессы. Тем не менее принципиальное разделение процессов на обратимые и необратимые по-прежнему существует; его только не следует воспринимать слишком буквально.
Выше мы затронули вопрос, который имеет решающее значение не только при общем анализе процессов, протекающих в природе, но и при определении степени применимости физических процессов. Этот вопрос связан с соотношением между теплотой и работой. Как мы видели, при адиабатическом сжатии газа затраченная работа затем может быть полностью получена обратно. При необратимых процессах, наоборот, по крайней мере часть затраченной механической работы полностью утрачивается и преобразуется в теплоту. При необратимых процессах вместо механической работы возникают какие-либо другие формы энергии, которые мы уже не можем использовать. По сравнению со всеми другими процессами обратимые всегда дают максимально возможную работу. Немного позже мы покажем, что это обстоятельство особенно важно для получения механической работы за счет тепловой энергии.
Лишь ценой большого напряжения сил, с помощью остроумных изобретений, люди научились превращать теплоту в полезную работу. Все естественные процессы непреодолимо развиваются в противоположном направлении: любая «освободившаяся» энергия превращается в тепло. Несомненно, что необратимость характерна для всех природных процессов, и, по-видимому, она составляет суть некоего совершенно универсального и всеобщего принципа. Однако пока нам все же недостает конкретной и «осязаемой» меры необратимости. Мы как-то уже обмолвились, что к области физики относится лишь то, что может быть измерено, но это положение не следует понимать чересчур буквально. Обычно заранее неизвестно, измеримо ли данное явление; это выясняется лишь в процессе изучения самого явления, в процессе выработки соответствующей техники измерений. Многое из того, о чем говорится сегодня в физике, вообще еще не поддается измерению.
Если нас интересуют наиболее яркие проявления необратимости, вернемся вновь к примеру с печкой. Полезная энергия отбирается от резервуара с высокой температурой (тлеющие угли) и переходит непосредственно к обогреваемому помещению, которое представляет собой единый «ненасытный» резервуар, имеющий более низкую температуру. В данном случае энергия не должна проходить через тепловую машину и выполнять полезную механическую работу, и ни одна калория тепла не исчезает и не разрушается. Однако возможность получить с помощью тепловой энергии механическую работу абсолютно исключена. Здесь не может быть и речи об обратимости процесса. Если рассматривать печку как тепловой двигатель, то его к.п.д. равен нулю; это еще раз показывает нам, сколь тесно связаны между собой понятия к.п.д. и обратимости.
Вернемся вновь к процессу Карно. Там мы получали соотношение Q2 /Q1 = Т2 /Т1, или, в другой форме,
Q1 /T1=Q2 /T2
Основатель термодинамики Рудольф Эмануэль Клаузиус (1822—1888) назвал это отношение энтропией:
S=Q/T
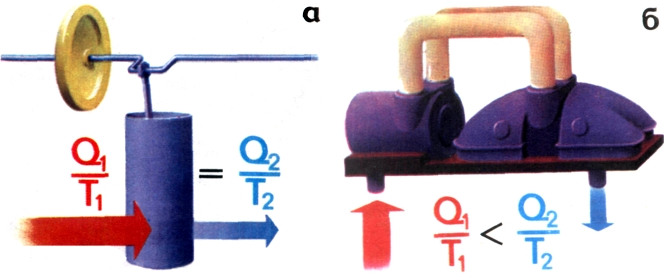
Смысл процессов, происходящих в цикле Карно, можно выразить коротко и ясно: энтропия, равная отношению количества теплоты Q к температуре Т, при которой это количество принимается (отдается), сохраняется постоянной (рис. 70, а).
 |
|
Рис. 70. Энтропия замкнутого цикла Карно остается постоянной (а). Энтропия паровой турбины возрастает (6).
|
Вот мы и нашли возможность однозначно различать обратимые и необратимые процессы. Если энтропия в ходе какого-то процесса сохраняется постоянной, то процесс обратим, если же возрастает — процесс необратим.
Для новичка понятие энтропии всегда представляет известную сложность. Читатель, как правило, не подготовлен к его восприятию, и сам ход рассуждений кажется ему весьма искусственным. Однако использование абстрактных понятий не мешает нам создать адекватную картину мира. Именно непрерывное расширение системы наших понятий все более раскрывает перед нами картину мира и делает ее все более универсальной. Вот почему открытие Клаузиусом количественной меры обратимости принадлежит к числу наиважнейших физических открытий.
Важность понятия энтропии выходит далеко за пределы круга вопросов, связанных с тепловыми машинами. В соответствующим образом модифицированной форме оно применимо и ко всем остальным процессам термодинамики. Поясним это на следующем простейшем примере: пусть имеется сосуд, содержащий 1 л воды при температуре 0°С. Сосуд стоит на газовой плите и должен быть нагрет до 100°С. Если мы будем рассматривать процесс нагревания с помощью своего рода «лупы времени», то «увидим», как при нагревании воды в нее через каждый градус «проскальзывает» одна калория. При этом каждая такая калория находит воду на 1°С горячее, чем ее предшественница. Каждая калория, отнесенная к соответствующей температуре, дает элементарную энтропию ΔQ/Т.
Полная энтропия воды будет равна сумме ![]() этих элементов S1 = 0,312 ккал/К.
этих элементов S1 = 0,312 ккал/К.
Совершенно аналогичный расчет мы можем провести для другого сосуда с 1 л воды, находящегося при 10°С, полагая при этом, что нагревание от 0 до 10 °С уже произошло каким-либо образом ранее; тогда мы получим S2 = 0,036 ккал/К. Теперь выльем горячую воду в холодную и хорошо перемешаем, реализовав таким образом необратимый процесс. И никаким способом нам не удастся вновь разделить полученную смесь на горячую и холодную части. Температура смеси составит 55°С, однако не будем измерять ее термометром, а лучше вычислим энтропию полученных 2 л теплой воды: она равна S3 = 0,367 ккал/К. Сумма энтропии до смешивания воды равна S1 + S2 = 0,348 ккал/К, и, следовательно, после смешивания полная энтропия возросла на ?S = 0,019 ккал/К. Таким образом, энтропия Клаузиуса оправдала себя как мера необратимости.
 |
|
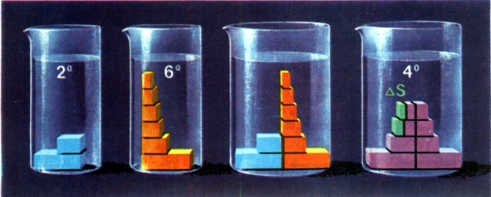
Рис. 71. Модель роста энтропии в процессе смешивания. |
На рис. 71 представлена грубая модель подобного про-цесса. Горячей воде сообщается 6 кал, и ее температура воз-растает на 6 град, а энтропия равна сумме 1/1 + + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 (ее изображают поставленные друг на друга кубики). Энтропия холодной воды при двух «градусах» показана всего лишь двумя кирпичиками и равна 1/1 + 1/2. Температура после смешивания равна среднему арифметическому этих температур: 4 град. На последнем рисунке по числу кубиков можно непосредственно сосчитать прирост энтропии всей смеси.
Итак, мы можем сделать следующий окончательный вывод: абсолютно обратимых процессов не существует и потому при всех доступных воображению физических процессах энтропия должна возрастать. В этом и заключается суть второго начала термодинамики: при всех процессах суммарная энтропия системы возрастает.
Слишком одностороннее прочтение этого закона легко приводит к недоразумению. Например, если сосуд с горячей водой самопроизвольно остывает, его энтропия S, как сумма элементов энтропии ΔQ/Т, разумеется, уменьшается. Однако следует рассматривать полную систему (вода + окружение). Отдаваемая водой теплота переходит к окружающим телам; по существу, здесь опять имеет место процесс смешивания, который мы уже рассматривали.
Тенденция к возрастанию энтропии определяет направление всех многообразных процессов в природе. Они протекают так, что полная энтропия системы увеличивается. Это всеобщий принцип, и, как мы уже видели, он дополняет закон сохранения энергии. Принцип энтропии «указывает» направление потока тепла или определенной химической реакции, он определяет, куда двигаться молекулам сжатого газа при наличии свободного пространства.
Не будь второго начала термодинамики, мы могли бы использовать, например, грандиозные запасы тепла Атлантического океана. Какой-нибудь хитроумный аппарат разделял бы подводимую в любом количестве массу воды на холодную и горячую. Далее горячая вода легко направлялась бы и питала крупную силовую установку, работающую «в паре» с этим таинственным разделительным аппаратом. Нечто подобное и называется вечным двигателем второго рода.
Разделение рабочей среды на горячую и холодную в принципе не невозможно и, по существу, происходит в каждом холодильнике. Однако последний должен при этом потреблять энергию, например механическую. Как показывает более детальный анализ, при этом требуется затратить больше работы, чем можно получить за счет разности температур охлаждающего агрегата. Вечный двигатель второго рода должен был бы состоять из охлаждающей машины и двигателя и работать изолированно длительное время. В поисках наиболее безупречной формулировки второго начала термодинамики Макс Планк пришел к следующему утверждению: «Невозможно создать периодически действующую машину, которая не приводит ни к каким иным результатам, кроме поднятия тяжестей и охлаждения теплового резервуара».
Ту часть данного запаса энергии, которую в принципе можно перевести в полезную работу, принято также называть свободной энергией. Отличительным признаком всех самопроизвольно протекающих процессов является то, что в ходе этих процессов свободная энергия системы непрерывно уменьшается. Там. где самопроизвольный процесс затруднен, его возникновению способствует человек. Это особенно ярко проявляется, например, при использовании энергии природного топлива. Ежеминутно на Земле сжигаются миллионы тонн угля и нефти. Энергия, первоначально запасенная в них в химической форме, превращается в тепловую; в этом качестве она кое-как используется и, в конечном счете, отправляется в атмосферу вместе с продуктами сгорания. Таким образом, делается все, чтобы предельно сократить запасы свободной энергии и приблизить энтропию к ее максимальному значению.
Не удивительно, что люди неоднократно размышляли над таким, казалось бы, роковым ходом событий. Ведь и Солнце в один прекрасный день израсходует все запасы свободной энергии, излучив их в разных направлениях, а наша Земля, холодная и лишенная какого-либо жизненного перепада температур, будет по-прежнему одиноко двигаться по орбите. И другие звезды, имеющие сегодня невообразимо высокие температуры и ярко светящиеся, однажды тоже погаснут. Все существующие в природе перепады температур выравняются. и все тела приобретут некоторую одинаковую среднюю температуру. При этом в соответствии с первым законом термодинамики полная энергия сохранится. Но исчезнет вся жизнь, ни одна машина не сможет прийти в движение, так как не будет свободной энергии для того, чтобы питать их. Столь мрачная картина тепловой смерти, угрожающей якобы всему нашему миру, основана на предположении о том, что второе начало термодинамики применимо без каких-либо ограничений во всех областях физики, во всех точках пространства и во все моменты времени. Однако это предположение в высшей степени сомнительно. Как мы еще увидим, в мире атомов и молекул существуют и другие возможности.
Вопрос о «тепловой смерти» Вселенной интенсивно дискутировался многие десятилетия. В статьях, посвященных этому вопросу, страстно обсуждались физические, философские и даже религиозные аспекты вопроса о приближающемся «конце света». В настоящее время страсти несколько остыли. Согласно недавним подсчетам, Солнце способно светить с неубывающей силой еще 1011 лет, а это по крайней мере в 10 раз превосходит время существования Солнечной системы до настоящего момента. Кроме того, расширяются масштабы использования ядерной энергии. Это свидетельствует о наступлении новой исторической эпохи, в которой на службу человеку будут поставлены практически не ограниченные запасы энергии.
Мы еще вернемся к этим вопросам, которые, по-видимому, вообще неисчерпаемы. Этими вопросами серьезно занимался уже Больцман, о чем свидетельствует такая шутка. В одной из бесед с Лошмидтом Больцман сказал о сущности второго начала термодинамики: «Когда выравняются все температуры, возникновение всякой разумной жизни станет вообще невозможным. В среде с одинаковой повсюду температурой никакой разум не может выдержать». Присутствовавший при этом физик Стефан лаконично заметил: «Теперь я понимаю, почему Ваши опыты в подвале с большими стеклянными трубками так плачевно провалились».
Теперь вновь вернемся к вопросу о происхождении теплоты. Она является выражением непрекращающегося движения молекул. Объектом нашего исследования по-прежнему останется идеальный газ. Если бы речь шла об одной частице, ее движение было бы прямым, как полет стрелы, и она не испытывала бы никакого сопротивления. В этом случае применимы законы классической механики. К сожалению, это не совсем так. Дело в том, что при обычных условиях среди молекул царит невообразимая «толкотня» — ведь их число огромно! Австрийский ученый Жозеф Лошмидт (1821 — 1895) впервые оценил его, и в его честь оно названо постоянной Лошмидта: в 1 см3 любого газа при О°С и давлении 1 атм, содержится NL = 27 · 1018 частиц.
Невозможно даже представить себе, насколько велико это число. Лорд Кельвин, по имени которого названа абсолютная шкала температур, привел однажды следующее сравнение. Возьмите стакан воды, молекулы которой каким-либо образом «помечены», и вылейте эту воду в океан. Через длительное время, примерно достаточное для того, чтобы вылитая вода равномерно распределилась по всему Мировому океану, зачерпните тем же стаканом в любом месте. Во взятой пробе вы обнаружите не менее 200 «меченых» молекул!
Ограничившись этим впечатляющим примером, напомним лишь заключительные слова из речи Больцмана, посвященной памяти его друга Лошмидта: «Итак, тело Лошмидта распалось на атомы, и с помощью открытого им закона мы можем подсчитать, на сколько именно. Речь памяти физика-экспериментатора не должна обойтись без демонстрации, и я позволил себе выписать соответствующее число на доске». Это была единица с двадцатью пятью нулями.
Как уже отмечалось, частицы газа никогда не пребывают в покое. В столпотворении миллиардов и миллиардов молекул неизбежны их соударения друг с другом. Каждую секунду одна молекула испытывает до 10 млрд. столкновений с другими молекулами (напомним, что газ рассматривается при обычных условиях). При этом не удается заметить ни малейшей потери энергии. Остается лишь удивляться тому, что средняя длина свободного пробега — расстояние, которое молекула в среднем пролетает в промежутке между соударениями, — составляет все же примерно 10-5 см, или около 1000 диаметров молекулы.
Эта гигантская «игра в бильярд» все же приводит к некоторому распределению скоростей молекул. В результате столкновений, испытываемых молекулами на их зигзагообразном пути, каждая отдельная частица то ускоряется, то тормозится. По воле случая одни частицы имеют большие скорости в течение продолжительного времени, тогда как другие почти покоятся. Ранее мы говорили, что температура тела связана со средним значением скорости, но в действительности встречаются всевозможные значения скоростей. Поэтому на молекулярном уровне понятие температуры теряет свой первоначальный смысл (ведь в таком случае каждая молекула должна была бы иметь свою «температуру»).
 |
|
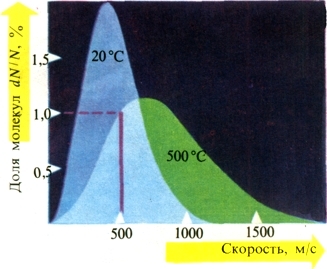
| Рис. 74. Распределение молекул азота по скоростям. Скорости измерены с точностью +5 м/с. |
Опираясь на законы теории вероятностей, Джеймс Клерк Максвелл вычислил распре-деление скоростей. На рис. 74 показан вид этой функции для азота при температурах 20 и 500°С. Из рисунка мы можем, например, установить, что при 500°С 1% всех молекул имеет скорости между 495 и 505 м/с (соответствующие значения помечены красным). Оценки такого рода, сделанные для больших «коллективов» частиц, называют статистическими. Каждому из нас неоднократно приходилось заполнять различ-ные опросные листы — разумеется, это тоже делается для статистических целей. Статистически можно также описать число костей у какого-нибудь сорта сельди или число зерен у какого-либо сорта хлебных злаков. Получаемые при этом кривые в целом достаточно сходны с максвелловской. Чтобы их построить и проанализировать, не требуется слишком больших математических способностей — в первую очередь нужно терпение для многочисленных подсчетов и записей.
Существенной особенностью движения отдельной частицы газа является его полная нерегулярность. Каждая частица движется по беспорядочно запутанным зигзагообразным траекториям. Подобно путнику, заблудившемуся в пустыне, она не в состоянии выбрать какое-либо определенное направление. Несчастный на исходе сил после долгих поисков пути может даже вновь вернуться в исходную точку. У молекул исход дела все же более благоприятный. С течением времени они все же смещаются в некотором направлении, причем среднее значение смещения можно подсчитать. В течение часа молекула воздуха проходит примерно около полуметра, но выбор направления по-прежнему остается делом чистого случая.
Однако именно это полное «незнание» в каждом отдельном случае приводит к совершенно определенным закономерностям статистического характера для совокупностей частиц. Основываясь на этом, математики создали и развили новую дисциплину — теорию вероятностей, которая приобретает все более важное значение. «Только благодаря господству случая мы могли сделать определенные выводы!» — сказал французский математик Анри Пуанкаре (1854—1912).
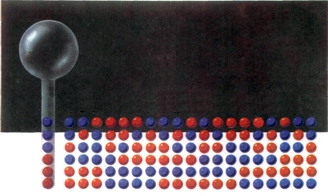
Хаотическое, беспорядочное движение молекул представляет собой идеальную арену для проявления случая; оно словно создано для применения теории вероятностей. Чтобы лучше уяснить, что при этом происходит, рассмотрим изображенный на рис. 77 стеклянный сосуд. «Молекулы содержащегося газа» представлены шестью деревянными шарами — тремя красными и тремя синими. Сначала они находятся в определенном порядке; теперь перевернем сосуд и «взболтаем» его содержимое. После возвращения шаров в трубку порядок их расположения, разумеется, изменяется (см., например, рис. 77, б). Всего возможно 20 различных комбинаций в размещении молекул, причем, если повторять опыт достаточно часто, рано или поздно осуществится каждая из них.
 |
|
Рис. 77. 20 возможных положений ситних и красных шариков. Каждое расположение имеет одинаковую вероятность w = 1/20. |
Назовем (весьма условно) начальное состояние порядком, а все остальные — беспорядком; тогда беспорядку будет соответствовать во много раз большая вероятность: 19/20 против 1/20. Это нетрудно понять, бегло взглянув на обычный письменный стол. Наведение порядка на нем требует значительных усилий и потому происходит сравнительно редко. Применительно к нашей модели газа мы можем сказать, что тенденция к молекулярному беспорядку значительно преобладает. Аналогично мы могли бы заполнить наш сосуд 2,7·1019 шарами (это число соответствует количеству молекул воздуха в 1 см3). Пусть, например, в начальном состоянии одна пятая трубки (нижняя) заполнена молекулами кислорода, а остальные четыре пятых — молекулами азота. Дальше все происходит совершенно самопроизвольно. В результате естественного движения молекул начинается процесс диффузии, он заканчивается лишь тогда, когда оба вида молекул полностью перемешиваются. Вероятность того, что они вновь разделяются на две различные части, исчезающе мала, так что процесс является необратимым.
При этом мы вновь соприкасаемся с необратимостью — основной проблемой термодинамики, — и для нее естественно ввести новую количественную меру. Такой мерой является термодинамическая вероятность состояния данной системы. Как мы уже знаем, при всех самопроизвольных процессах энтропия возрастает и стремится к максимальному значению. Если теперь нам удастся показать, что термодинамическая вероятность также стремится к максимальному значению, мы сможем вскрыть более глубокие взаимосвязи между физическими величинами.
Насколько маловероятны малейшие отклонения от макроскопически однородного распределения, показывает небольшой численный пример. Идея его принадлежит одному из первых Нобелевских лауреатов, французскому ученому Жану Перрену (1870—1942), известному своими работами в области молекулярного движения.
«Возьмем» 1 см3 обычного воздуха. Пусть из-за случайностей молекулярного движения небольшой уголок в этом объеме (например, 1 см3) в течение одной секунды остается пустым: в нем нет ни одной молекулы. Пусть в объеме (или в окружающем пространстве) находится некая достаточно заметная частица. Вероятность этой частицы не попасть в выделенный объем составляет 999/1000 =0,999 соответственно; вероятность того, что туда одновременно не попадет пять частиц составляет (0,999)5 (рис. 79).
 |
|
Рис. 79. Пять частиц не соберется вместе в выделенном объеме. |
Фактически же в рассматриваемом объеме находится не пять, а, согласно Лошмидту, 2,7 · 1016 частиц. В соответствии с нашим условием им всем одновременно строго воспрещается находиться в выделенном объеме, следовательно, полная вероятность такого состояния равна w = (0,999)2,7·10 000 000 000 000 000, или после логарифмирования и последующего потенцирования w = 1/1010 000 000 000 000. Таким образом, указанное состояние можно наблюдать один раз в течение 1010 000 000 000 000 с.
Со времени начала жизни на Земле прошло не более 1017 с, что записывается как единица с 17 нулями. Вычисленная же нами величина представляет собой единицу с 1013 нулями. Для записи такого числа понадобилось бы время, равное всей человеческой истории, а также продукция нескольких карандашных фабрик. Поэтому можно со спокойной совестью утверждать, что столь крупные пустоты в газах совершенно невозможны.
Вернемся теперь к обычному поведению идеальных газов. Все молекулы таких газов распределены равномерно по всему объему. Вероятность подобного распределения, как и энтропия замкнутой и предоставленной самой себе системы, стремится к максимальному значению. Как показал Людвиг Больцман, обе величины связаны между собой простым законом. Этот закон имеет чрезвычайно большое значение, и на могильной плите Больцмана выгравирована его формула:
S = k·lnw.
Итак, энтропия прямо пропорциональна натуральному логарифму термодинамической вероятности. Коэффициент пропорциональности к уже встречался нам в выражении, связывающем температуру и кинетическую энергию молекулы.
Принцип Больцмана вскрывает глубочайший смысл понятия энтропии. Все физические процессы протекают в направлении постепенного перехода от упорядоченного состояния к неупорядоченному, от состояний с меньшей вероятностью к состояниям более вероятным. Планк сказал: «При таком подходе второе начало термодинамики одним ударом лишается своего особого положения среди законов природы и принцип возрастания энтропии как хорошо обоснованный факт включается в физическую картину мира». Любой самопроизвольный процесс всегда протекает таким образом, что конечное состояние по сравнению с начальным имеет большую вероятность.
 |
|
Рис. 80. Охлаждение путём размагничивания парамагнитной соли. Упорядоченность элементарных магнитов в магнитном поле (а). Снятие упорядоченности при уменьшении магнитного поля содействует росту энтропии (б). |
На принципе возрастания молеку-лярного беспорядка основан метод, с помощью которого удалось получить самую низкую температуру. Парамаг-нитная соль (сульфат гадолиния) помещается в сильное магнитное поле, которое ориентирует все элементарные магниты в одном направлении (рис. 80). В результате образец переходит в состояние с наиболее высокой степенью порядка и, следовательно, с низшей энтропией. В то же время весь образец находится в сосуде с жидким гелием и благодаря этому имеет температуру порядка 1,3 К. При выключении магнитного поля упорядоченное состояние внезапно снимается и энтропия увеличивается скачком. Поскольку весь процесс происходит адиабатически, полная энергия системы сохраняется постоянной, и поэтому температура Т в силу соотношения S = Q/T с необходимостью должна уменьшиться. Таким способом удалось понизить температуру гелия до тысячных долей градуса по абсолютной шкале температур.